Llemma: El LLM Matemático que es Mejor que GPT-4

Name

Jennie Rose

Published on 30/4/2024

En el siempre cambiante campo de la inteligencia artificial, los modelos de lenguaje se han convertido en la piedra angular de numerosas aplicaciones, desde chatbots hasta generación de contenido. Sin embargo, cuando se trata de tareas especializadas como las matemáticas, no todos los modelos de lenguaje son iguales. Bienvenido a Llemma, un modelo innovador diseñado para abordar problemas matemáticos complejos con facilidad.

Si bien modelos como GPT-4 han avanzado significativamente en el procesamiento del lenguaje natural, fallan en el ámbito de las matemáticas. Este artículo tiene como objetivo arrojar luz sobre las capacidades únicas de Llemma y explorar por qué incluso gigantes como GPT-4 tropiezan cuando se trata de hacer cálculos.

¿Qué es Llemma?

Entonces, ¿qué es Llemma? Llemma es un modelo de lenguaje abierto que ha sido ajustado para especializarse en matemáticas. A diferencia de los modelos de propósito general, Llemma está equipado con herramientas computacionales que le permiten resolver problemas matemáticos complicados. Específicamente, utiliza intérpretes de Python y demostradores formales de teoremas para realizar cálculos y demostrar teoremas.

• Intérpretes de Python: Llemma puede ejecutar código Python para realizar cálculos complejos. Esta es una ventaja significativa sobre modelos como GPT-4, que carecen de la capacidad de interactuar con herramientas computacionales externas.

• Demostradores Formales de Teoremas: Estas herramientas permiten a Llemma demostrar teoremas matemáticos automáticamente. Esto es especialmente útil en la investigación académica y la modelización matemática.

La integración de estas herramientas computacionales distingue a Llemma de sus competidores. No solo entiende el lenguaje matemático, sino que también realiza cálculos y demuestra teoremas, ofreciendo una solución integral para tareas matemáticas.

¿Por qué GPT-4 falla en matemáticas? Tokenización.

Las limitaciones de GPT-4 en tareas matemáticas han sido objeto de discusión entre expertos y entusiastas por igual. Si bien es una potencia en el procesamiento del lenguaje natural, su rendimiento en cálculos matemáticos es menos que estelar.

La tokenización es un proceso crítico en cualquier modelo de lenguaje, pero es particularmente problemática en GPT-4 cuando se trata de números. El proceso de tokenización del modelo no proporciona representaciones únicas a los números, creando ambigüedad.

• Representaciones Ambiguas: Por ejemplo, el número "143" podría ser tokenizado como ["143"] o ["14", "3"], o cualquier otra combinación. Esta falta de una representación estándar dificulta que el modelo realice cálculos con precisión.

• Tokens Desperdiciados: Una solución alternativa podría ser tokenizar cada dígito por separado, pero este enfoque es ineficiente, ya que desperdicia tokens, que son un recurso valioso en los modelos de lenguaje.

Conjuntos de datos utilizados para el entrenamiento de Llemma

Los datos son el sustento de cualquier modelo de aprendizaje automático, y Llemma no es una excepción. Uno de los aspectos más destacados de Llemma es su uso de un conjunto de datos especializado conocido como AlgebraicStack. Este conjunto de datos comprende asombrosamente 11 mil millones de tokens de código relacionados específicamente con las matemáticas.

• Variedad de Tokens: El conjunto de datos incluye una amplia gama de conceptos matemáticos, desde álgebra hasta cálculo, proporcionando un terreno de entrenamiento rico para el modelo.

• Calidad de los Datos: Los tokens en AlgebraicStack son de alta calidad y rigurosamente evaluados, asegurando que el modelo se entrene con datos confiables.

El uso de un conjunto de datos tan especializado permite que Llemma alcance un nivel de conocimiento en matemáticas que es incomparable en la industria. No se trata solo de la cantidad de datos; se trata de la calidad y especificidad que hacen de Llemma un prodigio matemático.

¿Cómo funciona Llemma?

xVal: Soluciona el Problema de Tokenización de GPT-4

Una solución intrigante al problema de tokenización de GPT-4 es el concepto de xVal. Este enfoque sugiere el uso de un token genérico [NUM], que luego se escala por el valor real del número. Por ejemplo, el número "143" se tokenizaría como [NUM] y se escalaría por 143. Este método ha mostrado resultados prometedores en problemas de predicción de secuencias que son principalmente numéricos. Aquí tienes algunos puntos clave:

• Impulso de Rendimiento: El método de xVal ha demostrado una mejora significativa en el rendimiento en comparación con las técnicas de tokenización estándar. Ha mostrado una mejora de 70 veces en relación a los resultados básicos y una mejora de 2 veces en relación a los resultados sólidos en tareas de predicción de secuencias.

• Versatilidad: Un aspecto emocionante de xVal es su aplicabilidad potencial más allá de los modelos de lenguaje. Podría ser un cambio de juego para las redes neuronales profundas en problemas de regresión, ofreciendo una nueva forma de manejar datos numéricos.

Si bien xVal ofrece una luz de esperanza para mejorar las capacidades matemáticas de GPT-4, aún se encuentra en etapa experimental. Además, incluso si se implementa con éxito, solo serviría como una solución temporal para un problema más fundamental.

Submódulos y Experimentos en Llemma

Llemma no es solo un modelo independiente; forma parte de un ecosistema más amplio diseñado para ampliar los límites de lo que los modelos de lenguaje pueden lograr en matemáticas. El proyecto alberga una variedad de submódulos relacionados con superposición, ajuste fino y experimentos de demostración de teoremas.

• Submódulo de Superposición: Se enfoca en qué tan bien Llemma puede generalizar su entrenamiento para resolver problemas nuevos y no vistos.

• Submódulo de Ajuste Fino: Implica ajustar los parámetros del modelo para optimizar su rendimiento en tareas matemáticas específicas.

• Experimentos de Demostración de Teoremas: Estos están diseñados para probar la capacidad de Llemma para demostrar teoremas matemáticos complejos de forma automática.

Cada uno de estos submódulos contribuye a hacer de Llemma un modelo matemático completo y altamente capacitado. Sirven como bancos de pruebas para nuevas características y optimizaciones, asegurando que Llemma se mantenga a la vanguardia de la modelización del lenguaje matemático.

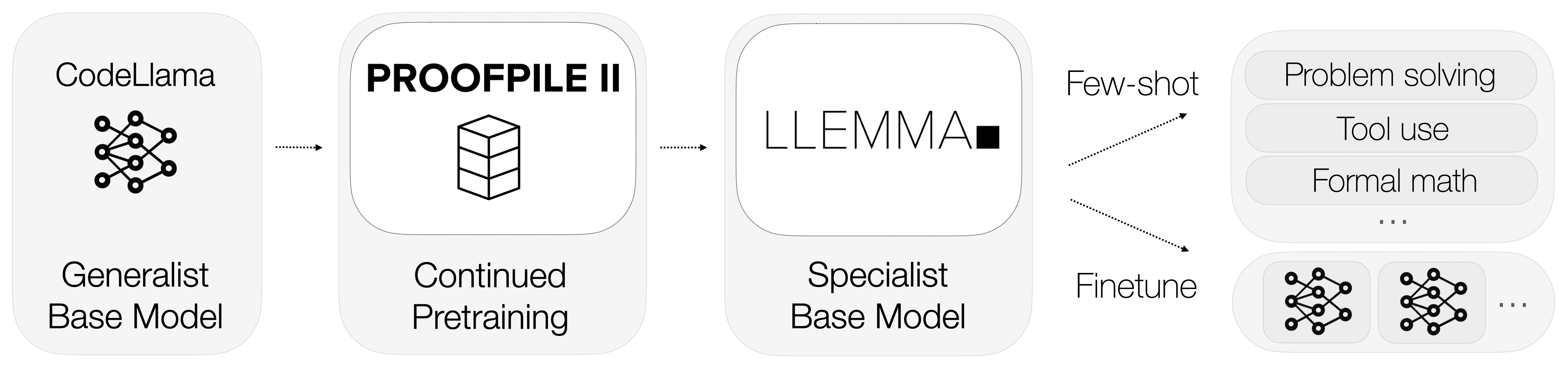
A estas alturas, debería quedar claro que Llemma no es solo otro modelo de lenguaje; es una herramienta especializada diseñada para destacar en el campo de las matemáticas. Su integración de herramientas computacionales, datos de entrenamiento especializados y experimentos en curso lo convierten en una fuerza formidable. En la siguiente sección, profundizaremos en por qué incluso modelos avanzados como GPT-4 tienen dificultades con las tareas matemáticas y cómo Llemma los deja atrás.

Llemma vs. GPT-4: ¿Cuál es mejor?

Cuando ponemos a Llemma y GPT-4 uno al lado del otro, las diferencias son evidentes. El enfoque especializado de Llemma en matemáticas, respaldado por herramientas computacionales y un conjunto de datos dedicado, le brinda una clara ventaja. Por otro lado, GPT-4, a pesar de su destreza en el procesamiento del lenguaje natural, se queda corto en tareas matemáticas debido a sus problemas de tokenización.

• Precisión: Llemma se jacta de tener un alto nivel de precisión tanto en cálculos como en demostración de teoremas, gracias a su entrenamiento especializado y herramientas computacionales. En contraste, GPT-4 tiene una tasa de precisión de casi 0% en multiplicación de 5 dígitos.

• Flexibilidad: La arquitectura de Llemma le permite adaptarse y destacarse en una variedad de tareas matemáticas, desde cálculos básicos hasta demostración de teoremas complejos. GPT-4 carece de este nivel de adaptabilidad cuando se trata de matemáticas.

• Eficiencia: El uso de conjuntos de datos especializados como AlgebraicStack asegura que Llemma se entrene con datos de alta calidad, lo que lo hace altamente eficiente en tareas matemáticas. GPT-4, con su entrenamiento de propósito general, no puede igualar este nivel de eficiencia.

En resumen, si bien GPT-4 puede ser un comodín en todo, Llemma es el maestro de uno: las matemáticas. Su enfoque especializado, junto con sus características avanzadas, lo convierte en el modelo ideal para cualquier tarea matemática. En la siguiente sección, concluiremos nuestra discusión y analizaremos qué depara el futuro para los modelos de lenguaje matemático como Llemma.

Conclusión: El futuro de los modelos de lenguaje matemático

Como hemos visto, Llemma es un testimonio de lo que los modelos de lenguaje especializados pueden lograr. Sus capacidades únicas para resolver problemas matemáticos y demostrar teoremas lo distinguen de los modelos de propósito general como GPT-4. Pero, ¿qué significa esto para el futuro de los modelos de lenguaje en matemáticas?

• Especialización sobre Generalización: El éxito de Llemma sugiere que el futuro puede estar en modelos de lenguaje especializados diseñados para tareas específicas. Si bien los modelos de propósito general tienen sus méritos, el nivel de experiencia que Llemma aporta es inigualable.

• Integración de Herramientas Computacionales: El uso de intérpretes de Python y demostradores de teoremas formales por parte de Llemma podría allanar el camino para futuros modelos que integren herramientas externas para tareas especializadas. Esto podría extenderse más allá de las matemáticas a campos como la física, la ingeniería e incluso la medicina.

• Tokenización Dinámica: Los problemas de tokenización enfrentados por GPT-4 resaltan la necesidad de métodos de tokenización más dinámicos y flexibles, como la solución xVal. Implementar técnicas de este tipo podría mejorar significativamente el rendimiento de los modelos de propósito general en tareas especializadas.

En resumen, Llemma sirve como un modelo para lo que los modelos de lenguaje especializados pueden y deben ser. No solo eleva el nivel de los modelos de lenguaje matemático, sino que también proporciona ideas valiosas que podrían beneficiar al campo más amplio de la inteligencia artificial.

Referencias

Para aquellos interesados en adentrarse más en el mundo de los modelos de lenguaje matemático, aquí hay algunas fuentes creíbles para leer más:

• Repositorio de GitHub del Proyecto Llemma (opens in a new tab)
• Conjunto de datos AlgebraicStack (opens in a new tab)
• Artículo de Investigación xVal (opens in a new tab)

¿Quieres conocer las últimas noticias de LLM? ¡Echa un vistazo a la última clasificación de LLM!