Llemma: Das mathematische LLM, das besser ist als GPT-4

Name

Jennie Rose

Published on 10.11.2023

In der sich ständig weiterentwickelnden Welt der künstlichen Intelligenz sind Sprachmodelle zu Eckpfeilern zahlreicher Anwendungen geworden, von Chatbots bis zur Erstellung von Inhalten. Bei spezialisierten Aufgaben wie Mathematik sind jedoch nicht alle Sprachmodelle gleich. Hier kommt Llemma ins Spiel, ein bahnbrechendes Modell, das komplexe mathematische Probleme mühelos lösen kann.

Während Modelle wie GPT-4 in der natürlichen Sprachverarbeitung bedeutende Fortschritte gemacht haben, sind sie im Bereich der Mathematik nicht besonders leistungsfähig. Dieser Artikel soll die einzigartigen Fähigkeiten von Llemma beleuchten und erklären, warum selbst Giganten wie GPT-4 Schwierigkeiten haben, komplexe mathematische Berechnungen durchzuführen.

Was ist Llemma?

Was ist also Llemma? Llemma ist ein offenes Sprachmodell, das speziell auf mathematische Aufgabenstellungen spezialisiert ist. Im Gegensatz zu allgemeinen Modellen verfügt Llemma über Rechentools, mit denen es komplexe mathematische Probleme lösen kann. Konkret nutzt es Python-Interpreter und formale Beweiser zur Durchführung von Berechnungen und zur Beweisführung.

• Python-Interpreter: Llemma kann Python-Code ausführen, um komplexe Berechnungen durchzuführen. Dies ist ein bedeutender Vorteil gegenüber Modellen wie GPT-4, die nicht über die Fähigkeit verfügen, mit externen Rechentools zu interagieren.

• Formale Beweiser: Diese Tools ermöglichen es Llemma, mathematische Theoreme automatisch zu beweisen. Dies ist besonders nützlich in der akademischen Forschung und bei mathematischer Modellierung.

Die Integration dieser Rechentools unterscheidet Llemma von seinen Konkurrenten. Es versteht nicht nur mathematische Sprache, sondern führt auch Berechnungen durch und beweist Theoreme. Es bietet eine umfassende Lösung für mathematische Aufgaben.

Warum GPT-4 in Mathe versagt? Tokenisierung.

Die Begrenzungen von GPT-4 bei mathematischen Aufgaben sind ein Thema, über das Experten und Enthusiasten gleichermaßen diskutieren. Obwohl es in der natürlichen Sprachverarbeitung eine Powerhouse ist, ist seine Leistung bei mathematischen Berechnungen weniger beeindruckend.

Tokenisierung ist ein entscheidender Prozess in jedem Sprachmodell, aber bei GPT-4 ist sie besonders problematisch, wenn es um Zahlen geht. Der Tokenisierungsprozess des Modells gibt Zahlen keine eindeutige Repräsentation, was zu Mehrdeutigkeiten führt.

• Mehrdeutige Repräsentation: Zum Beispiel könnte die Zahl "143" als ["143"] oder ["14", "3"] oder in einer anderen Kombination tokenisiert werden. Diese fehlende einheitliche Repräsentation erschwert dem Modell, genaue Berechnungen durchzuführen.

• Verschwendete Tokens: Eine Lösung könnte sein, jede Ziffer einzeln zu tokenisieren, aber dieser Ansatz ist ineffizient, da Tokens eine kostbare Ressource in Sprachmodellen sind.

Für Llemma verwendete Trainingsdaten

Daten sind das Lebenselixier eines jeden maschinellen Lernmodells, und Llemma bildet da keine Ausnahme. Einer der bemerkenswertesten Aspekte von Llemma ist die Verwendung eines spezialisierten Datensatzes namens AlgebraicStack. Dieser Datensatz enthält erstaunliche 11 Milliarden Code-Token, die speziell mit Mathematik in Verbindung stehen.

• Token-Vielfalt: Der Datensatz umfasst ein breites Spektrum mathematischer Konzepte, von Algebra bis hin zur Analysis, was einen reichen Übungsbereich für das Modell bietet.

• Datenqualität: Die Tokens in AlgebraicStack sind hochwertig und wurden sorgfältig geprüft, um sicherzustellen, dass das Modell auf zuverlässigen Daten trainiert wird.

Die Verwendung eines solchen spezialisierten Datensatzes ermöglicht es Llemma, ein Maß an Fachwissen in der Mathematik zu erreichen, das in der Branche einzigartig ist. Es geht nicht nur um die Menge der Daten, sondern auch um deren Qualität und Spezifität, die Llemma zu einem mathematischen Wunderkind machen.

Wie funktioniert Llemma?

xVal: Behebung des Tokenisierungsproblems von GPT-4

Eine interessante Lösung für das Tokenisierungsproblem von GPT-4 ist das Konzept von xVal. Dieser Ansatz schlägt vor, ein generisches [NUM]-Token zu verwenden, das dann mit dem tatsächlichen Wert der Zahl skaliert wird. Zum Beispiel würde die Zahl "143" als [NUM] tokenisiert und mit 143 skaliert. Diese Methode hat vielversprechende Ergebnisse bei Sequenzvorhersageproblemen gezeigt, die hauptsächlich numerisch sind. Hier sind einige wichtige Punkte:

• Leistungssteigerung: Die Methode xVal hat eine deutliche Verbesserung der Leistung im Vergleich zu Standard-Tokenisierungstechniken gezeigt. Sie erreicht eine 70-fache Verbesserung gegenüber Vanilla-Baselines und eine 2-fache Verbesserung gegenüber starken Baselines bei Sequenzvorhersageaufgaben.

• Vielseitigkeit: Ein aufregender Aspekt von xVal ist seine mögliche Anwendbarkeit nicht nur auf Sprachmodelle. Es könnte eine bahnbrechende Methode für tiefe neuronale Netze bei Regressionsproblemen sein und eine neue Möglichkeit bieten, numerische Daten zu verarbeiten.

Während xVal einen Hoffnungsschimmer für die Verbesserung der mathematischen Fähigkeiten von GPT-4 bietet, befindet es sich noch im experimentellen Stadium. Außerdem würde es selbst bei erfolgreicher Implementierung nur eine Lösung für ein grundlegenderes Problem sein.

Submodule und Experimente in Llemma

Llemma ist kein eigenständiges Modell, sondern Teil eines größeren Ökosystems, das darauf abzielt, die Grenzen dessen, was Sprachmodelle in der Mathematik erreichen können, auszuloten. Das Projekt umfasst eine Vielzahl von Submodulen, die sich mit Überschneidungen, Feinabstimmungen und Theorembeweis-Experimenten beschäftigen.

• Submodul für Überschneidungen: Hier geht es darum, wie gut Llemma seine Trainingsergebnisse auf neue, unbekannte Probleme verallgemeinern kann.

• Submodul für Feinabstimmung: Dabei werden die Parameter des Modells angepasst, um seine Leistung in bestimmten mathematischen Aufgaben zu optimieren.

• Beweisexperimente: Diese sind darauf ausgelegt, Llemma's Fähigkeit zu testen, komplexe mathematische Theoreme automatisch zu beweisen.

Jedes dieser Untermodule trägt dazu bei, Llemma zu einem vielseitigen und hochkompetenten mathematischen Modell zu machen. Sie dienen als Testumgebungen für neue Funktionen und Optimierungen und stellen sicher, dass Llemma weiterhin an vorderster Front der mathematischen Sprachmodellierung bleibt.

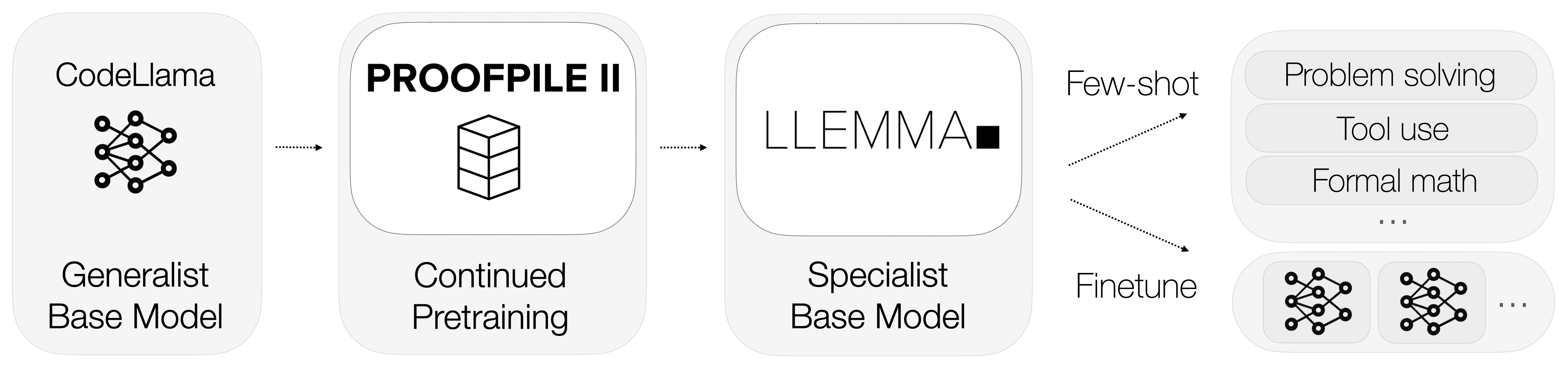
Es sollte mittlerweile klar sein, dass Llemma nicht nur ein weiteres Sprachmodell ist; es ist ein spezialisiertes Werkzeug, das sich im Bereich der Mathematik hervorragend bewährt. Die Integration von Rechenwerkzeugen, spezialisiertem Trainingsdaten und laufenden Experimenten macht es zu einer nicht zu unterschätzenden Kraft. Im nächsten Abschnitt werden wir genauer darauf eingehen, warum selbst fortschrittliche Modelle wie GPT-4 Schwierigkeiten mit mathematischen Aufgaben haben und wie Llemma sie in den Schatten stellt.

Llemma vs. GPT-4: Welches ist besser?

Wenn wir Llemma und GPT-4 direkt miteinander vergleichen, sind die Unterschiede deutlich. Llemma's spezialisiertes Fokus auf Mathematik, unterstützt von Rechenwerkzeugen und einem dedizierten Datensatz, verschafft ihm einen klaren Vorteil. Auf der anderen Seite schneidet GPT-4 trotz seiner Stärken in der natürlichen Sprachverarbeitung bei mathematischen Aufgaben aufgrund von Tokenisierungsproblemen schlecht ab.

• Genauigkeit: Llemma zeichnet sich durch eine hohe Genauigkeit sowohl bei Berechnungen als auch beim Beweisen von Theoremen aus, dank seines spezialisierten Trainings und seiner Rechenwerkzeuge. Im Gegensatz dazu hat GPT-4 eine nahezu 0%ige Genauigkeitsrate bei der 5-stelligen Multiplikation.

• Flexibilität: Die Architektur von Llemma ermöglicht es ihm, sich an verschiedene mathematische Aufgaben anzupassen und darin herausragende Leistungen zu erbringen, von einfachen Berechnungen bis hin zu komplexen Theorembeweisen. GPT-4 fehlt diese Art von Anpassungsfähigkeit in Bezug auf Mathematik.

• Effizienz: Durch die Verwendung spezialisierter Datensätze wie AlgebraicStack ist Llemma darauf trainiert, mit qualitativ hochwertigen Daten zu arbeiten und dadurch hocheffizient bei mathematischen Aufgaben zu sein. GPT-4 kann mit seinem allgemeinen Training dieses Maß an Effizienz nicht erreichen.

Zusammenfassend lässt sich sagen, dass GPT-4 zwar ein Generalist ist, aber Llemma der Spezialist: Mathematik. Sein spezialisierter Fokus, gepaart mit seinen fortschrittlichen Funktionen, macht es zum bevorzugten Modell für jede mathematische Aufgabe. Im nächsten Abschnitt werden wir unsere Diskussion abschließen und einen Blick auf die Zukunft mathematischer Sprachmodelle wie Llemma werfen.

Schlussfolgerung: Die Zukunft mathematischer Sprachmodelle

Wie wir gesehen haben, zeigt Llemma, was spezialisierte Sprachmodelle erreichen können. Seine einzigartigen Fähigkeiten, mathematische Probleme zu lösen und Theoreme zu beweisen, unterscheiden es von allgemein verwendbaren Modellen wie GPT-4. Aber was bedeutet das für die Zukunft von Sprachmodellen in der Mathematik?

• Spezialisierung statt Generalisierung: Der Erfolg von Llemma legt nahe, dass die Zukunft in spezialisierten Sprachmodellen liegt, die auf bestimmte Aufgaben zugeschnitten sind. Während allgemein verwendbare Modelle ihre Vorteile haben, ist das Fachwissen, das Llemma einbringt, unübertroffen.

• Integration von Rechenwerkzeugen: Llemma's Einsatz von Python-Interpretern und formalen Theorembeweisern könnte den Weg für zukünftige Modelle ebnen, die externe Werkzeuge für spezialisierte Aufgaben integrieren. Dies könnte über Mathematik hinausgehen und sich auch auf Bereiche wie Physik, Ingenieurwesen und sogar Medizin erstrecken.

• Dynamische Tokenisierung: Die Tokenisierungsprobleme, mit denen GPT-4 konfrontiert ist, zeigen den Bedarf an dynamischeren und flexibleren Tokenisierungsmethoden, wie z.B. der xVal-Lösung. Die Implementierung solcher Techniken könnte die Leistung von allgemein verwendbaren Modellen in spezialisierten Aufgaben erheblich verbessern.

Kurz gesagt fungiert Llemma als Blaupause für das, was spezialisierte Sprachmodelle sein können und sein sollten. Es setzt nicht nur den Maßstab für mathematische Sprachmodelle, sondern liefert auch wertvolle Erkenntnisse, die dem breiteren Bereich der künstlichen Intelligenz zugutekommen können.

Referenzen

Für alle, die tiefer in die Welt der mathematischen Sprachmodelle eintauchen möchten, gibt es hier einige vertrauenswürdige Quellen für weitere Informationen:

• Llemma Projekt GitHub Repository (opens in a new tab)
• AlgebraicStack Datensatz (opens in a new tab)
• xVal Forschungsarbeit (opens in a new tab)

Möchten Sie die neuesten Llemma-Nachrichten erfahren? Schauen Sie sich die neueste LLM-Rangliste an!