Llemma: Le LLM Mathématique Qui Est Mieux Que GPT-4

Name

Jennie Rose

Published on 30/04/2024

Dans le paysage en constante évolution de l'intelligence artificielle, les modèles linguistiques sont devenus la pierre angulaire de nombreuses applications, des chatbots à la génération de contenu. Cependant, lorsqu'il s'agit de tâches spécialisées comme les mathématiques, tous les modèles linguistiques ne sont pas créés égaux. Entrez Llemma, un modèle révolutionnaire conçu pour résoudre les problèmes mathématiques complexes avec facilité.

Alors que des modèles comme GPT-4 ont fait des avancées significatives dans le traitement du langage naturel, ils pèchent dans le domaine des mathématiques. Cet article vise à mettre en lumière les capacités uniques de Llemma et à expliquer pourquoi même des géants comme GPT-4 éprouvent des difficultés à traiter les chiffres.

Qu'est-ce que Llemma ?

Alors, qu'est-ce que Llemma ? Llemma est un modèle linguistique ouvert qui a été affiné pour se spécialiser dans les mathématiques. Contrairement aux modèles polyvalents, Llemma est équipé d'outils de calcul qui lui permettent de résoudre des problèmes mathématiques complexes. Plus précisément, il utilise des interpréteurs Python et des prouveurs de théorèmes formels pour effectuer des calculs et prouver des théorèmes.

• Interpréteurs Python : Llemma peut exécuter du code Python pour effectuer des calculs complexes. C'est un avantage significatif par rapport aux modèles comme GPT-4, qui n'ont pas la capacité d'interagir avec des outils de calcul externes.

• Prouveurs de Théorèmes Formels : Ces outils permettent à Llemma de prouver automatiquement des théorèmes mathématiques. Cela est particulièrement utile dans la recherche académique et la modélisation mathématique.

L'intégration de ces outils de calcul différencie Llemma de ses concurrents. Il comprend non seulement le langage mathématique, mais effectue également des calculs et prouve des théorèmes, offrant ainsi une solution complète pour les tâches mathématiques.

Pourquoi GPT-4 Échoue en Mathématiques ? La Tokenisation.

Les limites de GPT-4 dans les tâches mathématiques ont fait l'objet de discussions parmi les experts et les amateurs. Alors qu'il est puissant dans le traitement du langage naturel, ses performances dans les calculs mathématiques sont moins que satisfaisantes.

La tokenisation est un processus critique dans tout modèle linguistique, mais elle pose particulièrement problème dans GPT-4 lorsqu'il s'agit des chiffres. Le processus de tokenisation du modèle ne donne pas de représentations uniques aux chiffres, créant ainsi une ambiguïté.

• Représentations Ambiguës : Par exemple, le chiffre "143" pourrait être tokenisé en ["143"] ou ["14", "3"], ou toute autre combinaison. Ce manque de représentation standard rend difficile la précision des calculs pour le modèle.

• Tokens Gaspillés : Une solution de contournement pourrait consister à tokeniser chaque chiffre séparément, mais cette approche est inefficace car elle gaspille des tokens, qui sont une ressource précieuse dans les modèles linguistiques.

Jeux de données utilisés pour l'entraînement de Llemma

Les données sont le moteur de tout modèle d'apprentissage automatique, et Llemma ne fait pas exception. L'un des aspects les plus remarquables de Llemma est son utilisation d'un jeu de données spécialisé appelé AlgebraicStack. Ce jeu de données comprend un impressionnant 11 milliards de tokens de code spécifiquement liés aux mathématiques.

• Variété de Tokens : Le jeu de données inclut une large gamme de concepts mathématiques, de l'algèbre au calcul, offrant ainsi un terrain d'entraînement riche pour le modèle.

• Qualité des Données : Les tokens dans AlgebraicStack sont de haute qualité et rigoureusement sélectionnés, garantissant que le modèle est entraîné sur des données fiables.

L'utilisation d'un tel jeu de données spécialisé permet à Llemma d'atteindre un niveau d'expertise en mathématiques inégalé dans l'industrie. Il ne s'agit pas seulement de la quantité de données ; c'est la qualité et la spécificité qui font de Llemma un prodige mathématique.

Comment Llemma Fonctionne-t-il ?

xVal : Résoudre le Problème de Tokenisation de GPT-4

Une solution intrigante au problème de tokenisation de GPT-4 est le concept de xVal. Cette approche suggère d'utiliser un jeton générique [NUM], qui est ensuite mis à l'échelle en fonction de la valeur réelle du nombre. Par exemple, le nombre "143" serait tokenisé en [NUM] et mis à l'échelle par 143. Cette méthode a donné des résultats prometteurs dans les problèmes de prédiction de séquence qui sont principalement numériques. Voici quelques points clés :

• Amélioration des Performances : La méthode xVal a démontré une amélioration significative des performances par rapport aux techniques de tokenisation standard. Elle a montré une amélioration de 70x par rapport aux baselines standard et une amélioration de 2x par rapport aux baselines solides dans les tâches de prédiction de séquence.

• Polyvalence : Un aspect intéressant de xVal est son potentiel d'application au-delà des seuls modèles linguistiques. Il pourrait être révolutionnaire pour les réseaux neuronaux profonds dans les problèmes de régression, offrant une nouvelle façon de traiter les données numériques.

Bien que xVal offre une lueur d'espoir pour améliorer les capacités mathématiques de GPT-4, il est encore à l'étape expérimentale. De plus, même s'il est mis en œuvre avec succès, il ne servirait que de correctif à un problème plus fondamental.

Sous-modules et Expériences dans Llemma

Llemma n'est pas seulement un modèle indépendant ; il fait partie d'un écosystème plus large conçu pour repousser les limites de ce que les modèles linguistiques peuvent réaliser en mathématiques. Le projet héberge une variété de sous-modules liés aux chevauchements, au réglage fin et aux expériences de preuve de théorèmes.

• Sous-module de Chevauchement : Celui-ci se concentre sur la capacité de Llemma à généraliser son apprentissage pour résoudre de nouveaux problèmes non vus.

• Sous-module de Réglage Fin : Celui-ci implique de modifier les paramètres du modèle pour optimiser ses performances dans des tâches mathématiques spécifiques.

• Expériences de la démonstration de théorèmes: Elles sont conçues pour tester la capacité de Llemma à prouver automatiquement des théorèmes mathématiques complexes.

Chacun de ces sous-modules contribue à faire de Llemma un modèle mathématique complet et hautement performant. Ils servent de bancs d'essai pour de nouvelles fonctionnalités et optimisations, garantissant que Llemma reste à la pointe de la modélisation mathématique du langage.

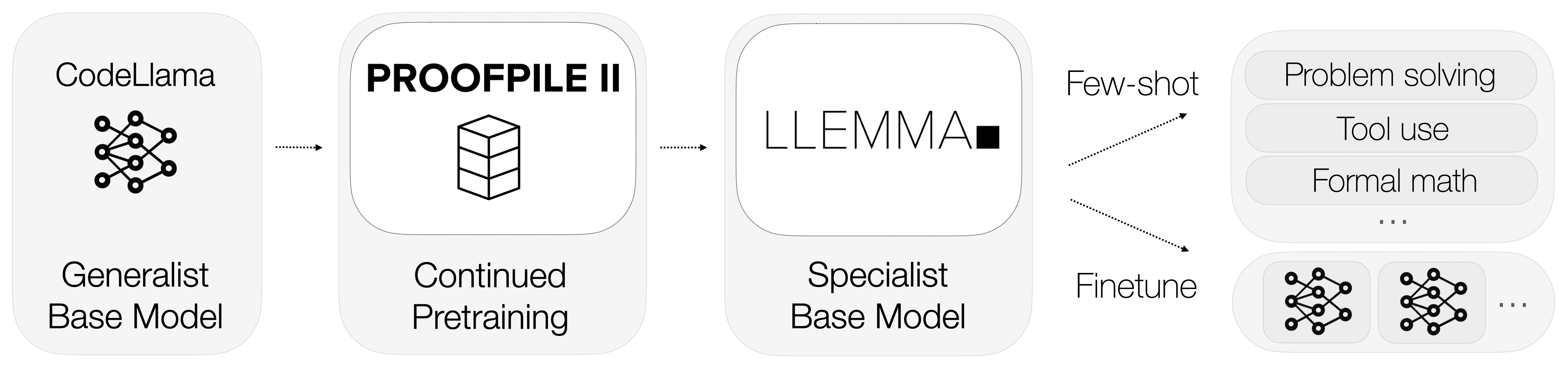
À présent, il devrait être clair que Llemma n'est pas seulement un autre modèle de langage ; c'est un outil spécialisé conçu pour exceller dans le domaine des mathématiques. Son intégration d'outils de calcul, de données de formation spécialisées et d'expériences en cours en font une force avec laquelle il faut compter. Dans la section suivante, nous examinerons pourquoi même les modèles avancés comme GPT-4 ont du mal avec les tâches mathématiques et comment Llemma les surpasse.

Llemma vs GPT-4 : Lequel est meilleur ?

Lorsque nous comparons Llemma et GPT-4 côte à côte, les différences sont frappantes. La spécialisation de Llemma en mathématiques, soutenue par des outils de calcul et un ensemble de données dédié, lui confère un avantage certain. En revanche, GPT-4, malgré ses compétences en traitement automatique du langage naturel, pèche dans les tâches mathématiques en raison de problèmes de tokenisation.

• Exactitude : Llemma se vante d'un haut niveau de précision tant dans les calculs que dans la démonstration de théorèmes, grâce à sa formation spécialisée et à ses outils de calcul. En revanche, GPT-4 a un taux de précision de près de 0% pour la multiplication de 5 chiffres.

• Flexibilité : L'architecture de Llemma lui permet de s'adapter et d'exceller dans une variété de tâches mathématiques, des calculs de base à la démonstration de théorèmes complexes. GPT-4 ne possède pas ce niveau d'adaptabilité en ce qui concerne les mathématiques.

• Efficacité : L'utilisation par Llemma d'ensembles de données spécialisés comme AlgebraicStack garantit qu'il est formé sur des données de haute qualité, ce qui le rend très efficace dans les tâches mathématiques. GPT-4, avec sa formation à usage général, ne peut pas rivaliser avec ce niveau d'efficacité.

En résumé, même si GPT-4 peut être un couteau suisse, Llemma est le maître d'un domaine : les mathématiques. Sa spécialisation, associée à ses fonctionnalités avancées, en fait le modèle de prédilection pour toute tâche mathématique. Dans la section suivante, nous conclurons notre discussion et examinerons ce que l'avenir réserve aux modèles de langage mathématique tels que Llemma.

Conclusion : L'avenir des modèles de langage mathématique

Comme nous l'avons vu, Llemma témoigne de ce que les modèles de langage spécialisés peuvent accomplir. Ses capacités uniques pour résoudre des problèmes mathématiques et démontrer des théorèmes le distinguent des modèles à usage général comme GPT-4. Mais qu'est-ce que cela signifie pour l'avenir des modèles de langage en mathématiques ?

• Spécialisation plutôt que généralisation : Le succès de Llemma suggère que l'avenir pourrait résider dans des modèles de langage spécialisés adaptés à des tâches spécifiques. Alors que les modèles à usage général ont leurs mérites, le niveau d'expertise que Llemma apporte est sans égal.

• Intégration d'outils de calcul : L'utilisation par Llemma d'interprètes Python et de prouveurs de théorèmes formels pourrait ouvrir la voie à des modèles futurs intégrant des outils externes pour des tâches spécialisées. Cela pourrait s'étendre au-delà des mathématiques à des domaines tels que la physique, l'ingénierie et même la médecine.

• Tokenisation dynamique : Les problèmes de tokenisation auxquels est confronté GPT-4 mettent en évidence la nécessité de méthodes de tokenisation plus dynamiques et flexibles, comme la solution xVal. La mise en œuvre de telles techniques pourrait améliorer considérablement les performances des modèles à usage général dans les tâches spécialisées.

En résumé, Llemma sert de modèle à suivre pour ce que les modèles de langage spécialisés peuvent et devraient être. Il élève non seulement la barre pour les modèles de langage mathématique, mais fournit également des connaissances précieuses qui pourraient bénéficier au domaine plus large de l'intelligence artificielle.

Références

Pour ceux qui souhaitent approfondir le monde des modèles de langage mathématique, voici quelques sources crédibles pour en savoir plus :

• Répertoire GitHub du projet Llemma (opens in a new tab)
• Ensemble de données AlgebraicStack (opens in a new tab)
• Article de recherche sur xVal (opens in a new tab)

Vous voulez connaître les dernières actualités sur LLM ? Consultez le dernier classement LLM !