Llemma: O LLM Matemático Que é Melhor Que o GPT-4
Published on

No cenário em constante evolução da inteligência artificial, modelos de linguagem se tornaram a base de inúmeras aplicações, desde chatbots até geração de conteúdo. No entanto, quando se trata de tarefas especializadas como matemática, nem todos os modelos de linguagem são iguais. Apresentamos Llemma, um modelo inovador projetado para lidar com problemas matemáticos complexos com facilidade.
Enquanto modelos como o GPT-4 fizeram avanços significativos no processamento de linguagem natural, eles falham no campo da matemática. Este artigo tem como objetivo iluminar as capacidades únicas do Llemma e explorar por que até mesmo gigantes como o GPT-4 falham ao lidar com cálculos matemáticos.
O que é Llemma?
Então, o que é Llemma? Llemma é um modelo de linguagem aberto que foi ajustado para se especializar em matemática. Ao contrário de modelos de propósito geral, Llemma vem equipado com ferramentas computacionais que permitem resolver problemas matemáticos intrincados. Especificamente, ele utiliza interpretadores Python e provadores formais de teoremas para realizar cálculos e provar teoremas.
-
Interpretadores Python: Llemma pode executar código Python para realizar cálculos complexos. Isso é uma grande vantagem em relação aos modelos como o GPT-4, que não possuem a capacidade de interagir com ferramentas computacionais externas.
-
Provadores Formais de Teoremas: Essas ferramentas permitem que Llemma prove automaticamente teoremas matemáticos. Isso é particularmente útil em pesquisa acadêmica e modelagem matemática.

A integração dessas ferramentas computacionais diferencia Llemma de seus concorrentes. Ele não apenas entende a linguagem matemática, mas também realiza cálculos e prova teoremas, oferecendo uma solução completa para tarefas matemáticas.
Por que o GPT-4 Falha em Matemática? Tokenização.
As limitações do GPT-4 em tarefas matemáticas têm sido um tema de discussão entre especialistas e entusiastas. Embora seja poderoso no processamento de linguagem natural, seu desempenho em cálculos matemáticos deixa a desejar.
A tokenização é um processo crítico em qualquer modelo de linguagem, mas é particularmente problemática no GPT-4 quando se trata de números. O processo de tokenização do modelo não atribui representações únicas aos números, criando ambiguidade.
-
Representações Ambíguas: Por exemplo, o número "143" pode ser tokenizado como ["143"] ou ["14", "3"], ou qualquer outra combinação. Essa falta de uma representação padrão dificulta o desempenho preciso de cálculos pelo modelo.
-
Tokens Desperdiçados: Uma solução alternativa poderia ser tokenizar cada dígito separadamente, mas essa abordagem é ineficiente, pois desperdiça tokens, que são um recurso valioso em modelos de linguagem.
Conjuntos de Dados Usados para o Treinamento do Llemma
Dados são o coração de qualquer modelo de aprendizado de máquina, e o Llemma não é exceção. Um dos aspectos mais notáveis do Llemma é o uso de um conjunto de dados especializado chamado AlgebraicStack. Este conjunto de dados contém incríveis 11 bilhões de tokens de código especificamente relacionados à matemática.
-
Variedade de Tokens: O conjunto de dados inclui uma ampla gama de conceitos matemáticos, desde álgebra até cálculo, oferecendo um ambiente de treinamento rico para o modelo.
-
Qualidade dos Dados: Os tokens em AlgebraicStack são de alta qualidade e rigorosamente verificados, garantindo que o modelo seja treinado com dados confiáveis.
O uso de um conjunto de dados tão especializado permite ao Llemma alcançar um nível de especialização em matemática que é incomparável na indústria. Não se trata apenas da quantidade de dados; trata-se da qualidade e especificidade que tornam o Llemma um prodígio matemático.
Como o Llemma Funciona?
xVal: Corrigindo o Problema de Tokenização do GPT-4
Uma solução intrigante para o problema de tokenização do GPT-4 é o conceito de xVal. Essa abordagem sugere o uso de um token genérico [NUM], que é então multiplicado pelo valor real do número. Por exemplo, o número "143" seria tokenizado como [NUM] e multiplicado por 143. Esse método tem mostrado resultados promissores em problemas de previsão de sequências que são principalmente numéricas. Aqui estão alguns pontos-chave:
-
Melhoria no Desempenho: O método xVal demonstrou uma melhoria significativa no desempenho em relação às técnicas de tokenização padrão. Ele apresentou uma melhoria de 70x em relação aos resultados básicos e uma melhoria de 2x em relação aos resultados fortes em tarefas de previsão de sequências.
-
Versatilidade: Um aspecto interessante do xVal é sua aplicabilidade potencial além dos modelos de linguagem. Ele poderia ser revolucionário para redes neurais profundas em problemas de regressão, oferecendo uma nova forma de lidar com dados numéricos.
Embora o xVal ofereça uma luz de esperança para melhorar as capacidades matemáticas do GPT-4, ele ainda está em estágio experimental. Além disso, mesmo se implementado com sucesso, ele serviria apenas como um paliativo para uma questão mais fundamental.
Submódulos e Experimentos no Llemma
O Llemma não é apenas um modelo independente; ele faz parte de um ecossistema maior projetado para empurrar os limites do que os modelos de linguagem podem alcançar em matemática. O projeto abriga uma variedade de submódulos relacionados a sobreposição, ajuste fino e experimentos de prova de teoremas.
-
Submódulo de Sobreposição: Isso se concentra em quão bem o Llemma pode generalizar seu treinamento para resolver problemas novos e invisíveis.
-
Submódulo de Ajuste Fino: Isso envolve ajustar os parâmetros do modelo para otimizar seu desempenho em tarefas matemáticas específicas.
-
Experimentos de Prova de Teorema: Estes são projetados para testar a capacidade de Llemma de provar teoremas matemáticos complexos automaticamente.
Cada um desses submódulos contribui para tornar Llemma um modelo matemático altamente capaz e equilibrado. Eles servem como bancos de testes para novos recursos e otimizações, garantindo que Llemma permaneça na vanguarda da modelagem matemática.
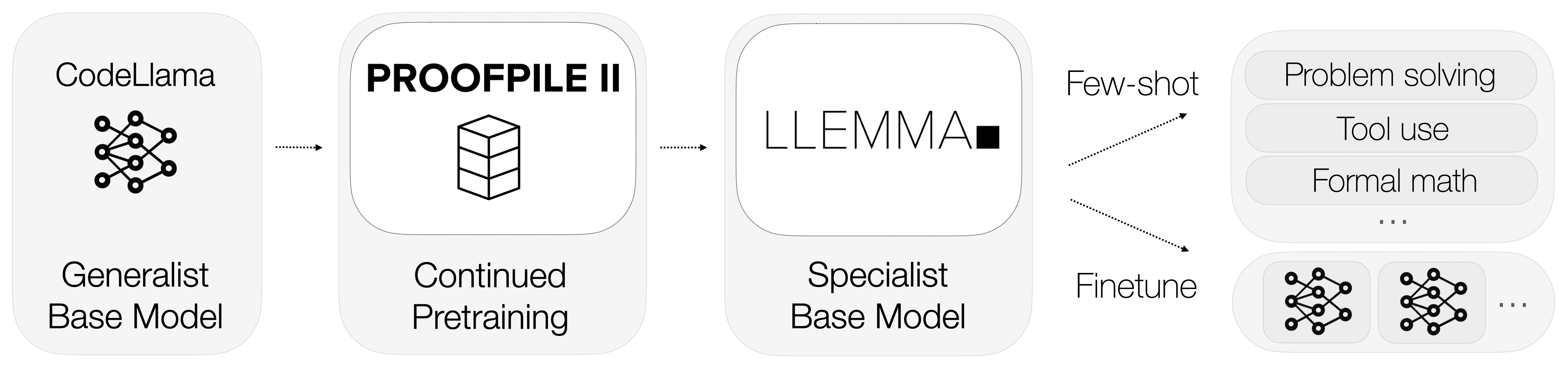
Agora deve estar claro que Llemma não é apenas mais um modelo de linguagem; é uma ferramenta especializada projetada para se destacar no campo da matemática. Sua integração de ferramentas computacionais, dados de treinamento especializados e experimentos contínuos o tornam uma força a ser reconhecida. Na próxima seção, vamos explorar por que até mesmo modelos avançados como GPT-4 têm dificuldade com tarefas matemáticas e como Llemma sai na frente.
Llemma vs. GPT-4: Qual é melhor?
Quando colocamos Llemma e GPT-4 lado a lado, as diferenças são evidentes. O foco especializado de Llemma em matemática, respaldado por ferramentas computacionais e um conjunto de dados dedicado, dá a ele uma clara vantagem. Por outro lado, o GPT-4, apesar de sua destreza no processamento de linguagem natural, fica aquém nas tarefas matemáticas devido aos seus problemas de tokenização.
-
Precisão: Llemma possui um alto nível de precisão tanto em cálculos quanto em prova de teoremas, graças ao seu treinamento especializado e ferramentas computacionais. Em contraste, GPT-4 tem uma taxa de precisão quase zero em multiplicação de 5 dígitos.
-
Flexibilidade: A arquitetura do Llemma permite que ele se adapte e se destaque em uma variedade de tarefas matemáticas, desde cálculos básicos até prova de teoremas complexos. O GPT-4 não possui esse nível de adaptabilidade quando se trata de matemática.
-
Eficiência: O uso de conjuntos de dados especializados como o AlgebraicStack pelo Llemma garante que ele seja treinado em dados de alta qualidade, tornando-se altamente eficiente em tarefas matemáticas. O GPT-4, com seu treinamento de propósito geral, não pode alcançar esse nível de eficiência.
Em resumo, enquanto o GPT-4 pode ser um curinga, o Llemma é o mestre em um único campo: matemática. Seu foco especializado, juntamente com seus recursos avançados, faz dele o modelo ideal para qualquer tarefa matemática. Na próxima seção, concluiremos nossa discussão e veremos o que o futuro reserva para os modelos de linguagem matemática, como o Llemma.
Conclusão: O Futuro dos Modelos de Linguagem Matemática
Como vimos, o Llemma é um testemunho do que os modelos de linguagem especializados podem alcançar. Suas capacidades únicas para resolver problemas matemáticos e provar teoremas destacam-no de modelos de propósito geral como o GPT-4. Mas o que isso significa para o futuro dos modelos de linguagem na matemática?
-
Especialização em vez de Generalização: O sucesso do Llemma sugere que o futuro pode estar em modelos de linguagem especializados adaptados para tarefas específicas. Embora os modelos de propósito geral tenham seus méritos, o nível de expertise que o Llemma traz para a mesa é incomparável.
-
Integração de Ferramentas Computacionais: O uso de interpretadores Python e provadores formais pelo Llemma pode abrir caminho para modelos futuros que integram ferramentas externas para tarefas especializadas. Isso pode se estender além da matemática para áreas como física, engenharia e até medicina.
-
Tokenização Dinâmica: Os problemas de tokenização enfrentados pelo GPT-4 destacam a necessidade de métodos de tokenização mais dinâmicos e flexíveis, como a solução xVal. Implementar tais técnicas pode melhorar significativamente o desempenho de modelos de propósito geral em tarefas especializadas.
Resumindo, o Llemma serve como um modelo para o que os modelos de linguagem especializados podem e devem ser. Ele não apenas eleva o padrão para modelos de linguagem matemática, mas também fornece insights valiosos que podem beneficiar o campo mais amplo de inteligência artificial.
Referências
Para aqueles interessados em aprofundar no mundo dos modelos matemáticos de linguagem, aqui estão algumas fontes confiáveis para leitura adicional:
- Repositório GitHub do Projeto Llemma (opens in a new tab)
- Conjunto de Dados AlgebraicStack (opens in a new tab)
- Artigo de Pesquisa xVal (opens in a new tab)
Quer ficar por dentro das últimas notícias do LLM? Confira a classificação mais recente do LLM!
