Llemma: GPT-4よりも優れた数学のLLM
Published on

人工知能の絶え間ない進化の中で、言語モデルはチャットボットからコンテンツ生成まで、数々のアプリケーションの基盤となっています。しかし、数学のような特殊なタスクにおいては、すべての言語モデルが同じように作成されているわけではありません。Llemmaが登場します。複雑な数学問題に簡単に取り組むために設計された画期的なモデルです。
GPT-4のようなモデルは自然言語処理で大きな進歩を遂げていますが、数学の領域では力不足です。本記事では、Llemmaの独自の能力に光を当て、GPT-4のような巨大な存在でも数式処理に苦労する理由を探求します。
Llemmaとは?
それでは、Llemmaとは何でしょうか?Llemmaは数学に特化したオープンな言語モデルです。汎用のモデルとは異なり、Llemmaは複雑な数学の問題を解決するための計算ツールを備えています。具体的には、Pythonインタプリタと形式的な定理証明器を利用して計算を行い、定理を証明します。
-
Pythonインタプリタ:LlemmaはPythonコードを実行して複雑な計算を行うことができます。これは、外部の計算ツールとの連携ができないGPT-4のようなモデルに比べて重要な利点です。
-
形式的な定理証明器:これらのツールにより、Llemmaは数学の定理を自動的に証明することができます。これは学術研究や数学モデリングに特に有用です。

これらの計算ツールの統合により、Llemmaは競合他社と一線を画しています。数学的な言語を理解するだけでなく、計算を実行し定理を証明することで、数学的なタスクに対する包括的な解決策を提供します。
GPT-4の数学への失敗?トークン化。
GPT-4の数学的なタスクへの限界は、専門家や愛好家の間でも議論の対象となっています。自然言語処理では強力な存在ですが、数学的な計算では優れない性能を示します。
トークン化はあらゆる言語モデルにおいて重要なプロセスですが、数に関しては特にGPT-4に問題があります。モデルのトークン化プロセスは数に対して一意な表現を与えず、曖昧さを生じさせます。
-
曖昧な表現:たとえば、数字の「143」は["143"]や["14", "3"]など、他の組み合わせでもトークン化されることがあります。この標準的な表現の欠如は、モデルが正確な計算を行うのを困難にします。
-
トークンの浪費:各桁を個別にトークン化するという回避策も考えられますが、このアプローチは非効率であり、言語モデルでは貴重なリソースであるトークンを浪費してしまいます。
Llemmaのトレーニングに使用されるデータセット
データは機械学習モデルの命でもあり、Llemmaも例外ではありません。Llemmaの最も注目すべき側面の一つは、AlgebraicStackという特殊なデータセットの使用です。このデータセットには、数学に関連する約110億トークンのコードが含まれています。
-
トークンの多様性:このデータセットには、代数から微積分まで幅広い数学的な概念が含まれており、モデルの訓練に豊かな環境を提供しています。
-
データの品質:AlgebraicStackのトークンは高品質で厳格に検証されており、モデルの訓練が信頼性のあるデータで行われます。
このような特殊なデータセットの使用により、Llemmaは業界で類を見ない数学の専門知識を実現しています。データの量だけでなく、品質と特異性がLlemmaを数学の天才とするのです。
Llemmaの動作原理は?
xVal: GPT-4のトークン化問題の解消
GPT-4のトークン化問題に対する興味深い解決策の一つは、xValという概念です。このアプローチでは、実際の数値でスケーリングされる一般的な[NUM]トークンを使用します。たとえば、「143」という数字は[NUM]としてトークン化され、その後で143でスケーリングされます。この方法は主に数値が含まれるシーケンス予測問題で有望な結果を示しています。以下にいくつかの重要なポイントを示します。
-
パフォーマンス向上:xValメソッドは、標準のトークン化技術に比べて、パフォーマンスを大幅に向上させました。シーケンス予測タスクでは、バニラのベースラインに比べて70倍の改善、強力なベースラインに比べて2倍の改善が見られました。
-
汎用性:xValの興味深い側面の一つは、言語モデルに限らず、深層ニューラルネットワークにおいて、数値データを処理する新しい方法を提供できる可能性です。
xValはGPT-4の数学的な能力を向上させる一筋の希望を与えていますが、まだ実験段階です。さらに、成功裏に実装された場合でも、それはより根本的な問題への応急処置にすぎません。
Llemmaのサブモジュールと実験
Llemmaは単独のモデルなだけでなく、数学で言語モデルが達成できる領域を広げるために設計された大規模なエコシステムの一部です。このプロジェクトには、オーバーラップ、ファインチューニング、定理証明実験に関連するさまざまなサブモジュールがあります。
- Theorem Proving Experiments: これらは、レンマが複雑な数学の定理を自動的に証明する能力をテストするために設計されています。
これらのサブモジュールは、Llemmaをバランスの取れた優れた数学モデルにするのに貢献しています。新機能や最適化のためのテストベッドとして機能し、Llemmaが数学の言語モデリングの最先端に位置することを保証します。
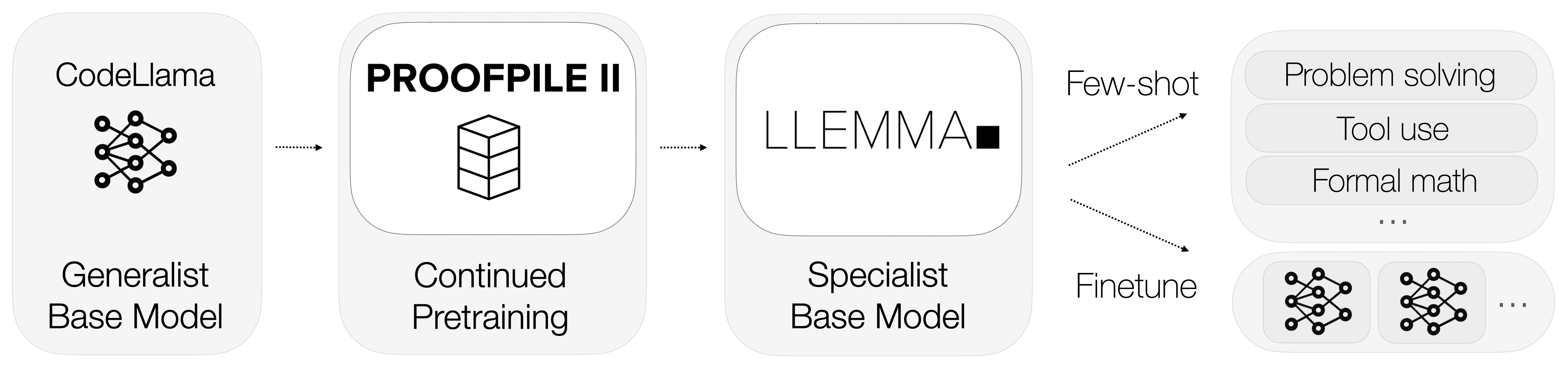
今さら言うまでもなく、Llemmaはただの言語モデルではありません。それは数学の領域で優れたパフォーマンスを発揮するために特化したツールです。計算ツール、専門のトレーニングデータ、継続的な実験の統合により、Llemmaは強力な存在となっています。次のセクションでは、GPT-4のような高度なモデルでも数学の課題に苦戦する理由と、Llemmaがそれを圧倒する方法について詳しく見ていきましょう。
Llemma vs. GPT-4:どちらが優れているのか?
LlemmaとGPT-4を並べて比較すると、その違いは明白です。計算ツールと専用のデータセットに支えられたLlemmaの数学への特化は、明確な優位性を持っています。一方、GPT-4は自然言語処理の能力に優れているものの、トークン化の問題から数学の課題には対応できていません。
-
正確さ: Llemmaは、専門のトレーニングと計算ツールにより、計算および定理の証明の両方で高い正確性を誇っています。対照的に、GPT-4は5桁の乗算の正確性率がほぼ**0%**です。
-
柔軟性: Llemmaのアーキテクチャは、基本的な計算から複雑な定理の証明まで、さまざまな数学的課題に適応して優れた能力を発揮することができます。数学に関しては、GPT-4はこのような適応性に欠けています。
-
効率性: Llemmaは、AlgebraicStackなどの専門データセットを使用することで、高品質のデータでトレーニングされているため、数学の課題で非常に効率的です。汎用的なトレーニングを行うGPT-4は、このレベルの効率性には及びません。
要約すると、GPT-4は何でも屋かもしれませんが、Llemmaは数学の王者です。その特化した焦点と高度な機能により、任意の数学の課題におけるモデルの選択肢となります。次のセクションでは、議論をまとめ、Llemmaのような数学の言語モデルの将来について考察していきます。
結論:数学の言語モデルの未来
Llemmaの成功は、専門の言語モデルがどれほど成果を上げることができるかを示すものです。数学の問題を解決し、定理を証明するユニークな機能により、LlemmaはGPT-4のような汎用モデルとは一線を画しています。しかし、これは数学の分野における言語モデルの未来についてどのような意味を持つのでしょうか?
-
専門性と一般化: Llemmaの成功は、将来は特定のタスクに特化した専門の言語モデルに注目が集まる可能性があることを示唆しています。汎用的なモデルにはメリットがありますが、Llemmaがもたらす専門知識のレベルは比類がありません。
-
計算ツールの統合: LlemmaがPythonインタプリタと形式的な定理証明器を使用していることは、将来のモデルが特化したタスクに外部ツールを統合する道を開く可能性があります。これは数学に限らず、物理学、エンジニアリング、さらには医学などの分野にも拡大していくかもしれません。
-
ダイナミックなトークン化: GPT-4が直面するトークン化の問題は、よりダイナミックで柔軟なトークン化手法(たとえばxValソリューション)の必要性を示しています。このような技術を実装することで、汎用モデルの特化したタスクにおけるパフォーマンスを大幅に向上させることができるでしょう。
要するに、Llemmaは専門の言語モデルがどのようなものであるべきかを示す設計図となっています。それは数学の言語モデルの基準を高めるだけでなく、人工知能のより広範な分野にも価値ある洞察を提供しています。
参考文献
数学の言語モデルの世界に深く関わりたい方のために、さらなる研究資料として信頼性のある情報源を以下に示します:
- LlemmaプロジェクトのGitHubリポジトリ (opens in a new tab)
- AlgebraicStackデータセット (opens in a new tab)
- xValの研究論文 (opens in a new tab)
LLMの最新ニュースを知りたいですか?最新のLLMリーダーボードをチェックしてください!
