Llemma: The Mathematical LLM That is Better Than GPT-4
Published on

In the ever-evolving landscape of artificial intelligence, language models have become the cornerstone of numerous applications, from chatbots to content generation. However, when it comes to specialized tasks like mathematics, not all language models are created equal. Enter Llemma, a game-changing model designed to tackle complex mathematical problems with ease.
While models like GPT-4 have made significant strides in natural language processing, they fall short in the realm of mathematics. This article aims to shed light on the unique capabilities of Llemma and explore why even giants like GPT-4 stumble when it comes to crunching numbers.
What is Llemma?
So, what is Llemma? Llemma is an open language model that's been fine-tuned to specialize in mathematics. Unlike general-purpose models, Llemma is equipped with computational tools that enable it to solve intricate mathematical problems. Specifically, it utilizes Python interpreters and formal theorem provers to carry out calculations and prove theorems.
-
Python Interpreters: Llemma can execute Python code to perform complex calculations. This is a significant advantage over models like GPT-4, which lack the ability to interact with external computational tools.
-
Formal Theorem Provers: These tools allow Llemma to prove mathematical theorems automatically. This is particularly useful in academic research and mathematical modeling.

The integration of these computational tools sets Llemma apart from its competitors. It not only understands mathematical language but also performs calculations and proves theorems, offering a comprehensive solution for mathematical tasks.
Why GPT-4 Fails at Math? Tokenization.
The limitations of GPT-4 in mathematical tasks have been a subject of discussion among experts and enthusiasts alike. While it's a powerhouse in natural language processing, its performance in mathematical calculations is less than stellar.
Tokenization is a critical process in any language model, but it's particularly problematic in GPT-4 when it comes to numbers. The model's tokenization process does not give unique representations to numbers, creating ambiguity.
-
Ambiguous Representations: For example, the number "143" could be tokenized as ["143"] or ["14", "3"], or any other combination. This lack of a standard representation makes it difficult for the model to perform calculations accurately.
-
Wasted Tokens: One workaround could be to tokenize each digit separately, but this approach is inefficient as it wastes tokens, which are a precious resource in language models.
Datasets used for Training for Llemma
Data is the lifeblood of any machine learning model, and Llemma is no exception. One of the most remarkable aspects of Llemma is its use of a specialized dataset known as AlgebraicStack. This dataset comprises a staggering 11 billion tokens of code specifically related to mathematics.
-
Token Variety: The dataset includes a wide range of mathematical concepts, from algebra to calculus, providing a rich training ground for the model.
-
Data Quality: The tokens in AlgebraicStack are high-quality and rigorously vetted, ensuring that the model is trained on reliable data.
The use of such a specialized dataset enables Llemma to achieve a level of expertise in mathematics that is unparalleled in the industry. It's not just about the quantity of data; it's about the quality and specificity that make Llemma a mathematical prodigy.
How Does Llemma Work?
xVal: Fix the GPT-4 Tokenization Problem
One intriguing solution to GPT-4's tokenization problem is the concept of xVal. This approach suggests using a generic [NUM] token, which is then scaled by the actual value of the number. For example, the number "143" would be tokenized as [NUM] and scaled by 143. This method has shown promising results in sequence prediction problems that are primarily numeric. Here are some key points:
-
Performance Boost: The xVal method has demonstrated a significant improvement in performance over standard tokenization techniques. It has shown a 70x improvement over vanilla baselines and a 2x improvement over strong baselines in sequence prediction tasks.
-
Versatility: One exciting aspect of xVal is its potential applicability beyond just language models. It could be a game-changer for deep neural networks in regression problems, offering a new way to handle numerical data.
While xVal offers a glimmer of hope for improving GPT-4's mathematical capabilities, it's still in the experimental stage. Moreover, even if successfully implemented, it would only serve as a patch to a more fundamental issue.
Submodules and Experiments in Llemma
Llemma is not just a standalone model; it's part of a larger ecosystem designed to push the boundaries of what language models can achieve in mathematics. The project hosts a variety of submodules related to overlap, fine-tuning, and theorem proving experiments.
-
Overlap Submodule: This focuses on how well Llemma can generalize its training to solve new, unseen problems.
-
Fine-Tuning Submodule: This involves tweaking the model's parameters to optimize its performance in specific mathematical tasks.
-
Theorem Proving Experiments: These are designed to test Llemma's ability to prove complex mathematical theorems automatically.
Each of these submodules contributes to making Llemma a well-rounded and highly capable mathematical model. They serve as testbeds for new features and optimizations, ensuring that Llemma remains at the cutting edge of mathematical language modeling.
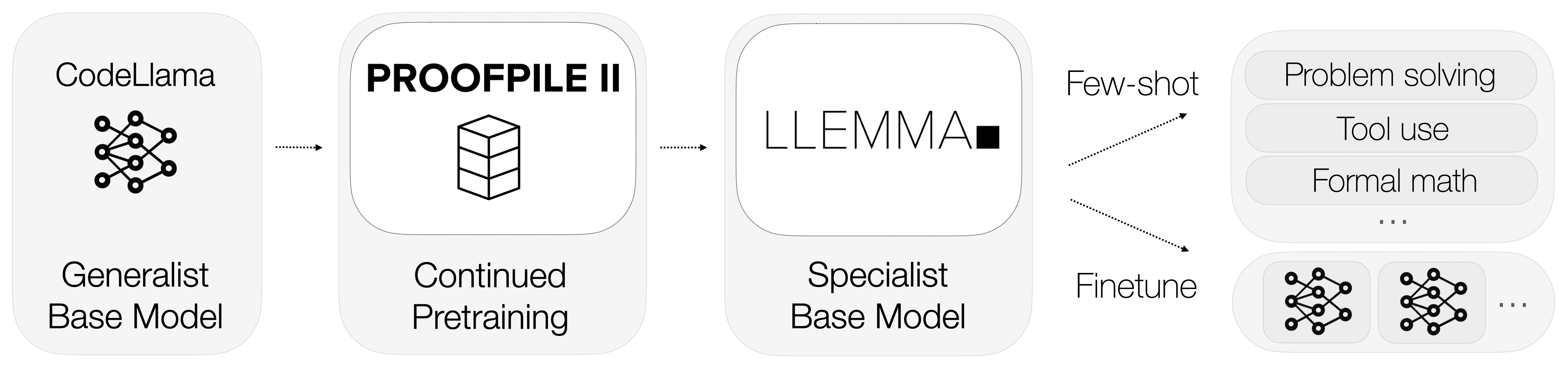
By now, it should be clear that Llemma is not just another language model; it's a specialized tool designed to excel in the field of mathematics. Its integration of computational tools, specialized training data, and ongoing experiments make it a force to be reckoned with. In the next section, we'll delve into why even advanced models like GPT-4 struggle with mathematical tasks and how Llemma leaves them in the dust.
Llemma vs. GPT-4: Which is Better?
When we put Llemma and GPT-4 side by side, the differences are stark. Llemma's specialized focus on mathematics, backed by computational tools and a dedicated dataset, gives it a clear edge. On the other hand, GPT-4, despite its prowess in natural language processing, falls short in mathematical tasks due to its tokenization issues.
-
Accuracy: Llemma boasts a high level of accuracy in both calculations and theorem proving, thanks to its specialized training and computational tools. In contrast, GPT-4 has a nearly 0% accuracy rate on 5-digit multiplication.
-
Flexibility: Llemma's architecture allows it to adapt and excel in a variety of mathematical tasks, from basic calculations to complex theorem proving. GPT-4 lacks this level of adaptability when it comes to mathematics.
-
Efficiency: Llemma's use of specialized datasets like AlgebraicStack ensures that it is trained on high-quality data, making it highly efficient in mathematical tasks. GPT-4, with its general-purpose training, cannot match this level of efficiency.
In summary, while GPT-4 may be a jack-of-all-trades, Llemma is the master of one: mathematics. Its specialized focus, coupled with its advanced features, makes it the go-to model for any mathematical task. In the next section, we'll wrap up our discussion and look at what the future holds for mathematical language models like Llemma.
Conclusion: The Future of Mathematical Language Models
As we've seen, Llemma stands as a testament to what specialized language models can achieve. Its unique capabilities in solving mathematical problems and proving theorems set it apart from general-purpose models like GPT-4. But what does this mean for the future of language models in mathematics?
-
Specialization Over Generalization: The success of Llemma suggests that the future may lie in specialized language models tailored for specific tasks. While general-purpose models have their merits, the level of expertise that Llemma brings to the table is unparalleled.
-
Integration of Computational Tools: Llemma's use of Python interpreters and formal theorem provers could pave the way for future models that integrate external tools for specialized tasks. This could extend beyond mathematics to fields like physics, engineering, and even medicine.
-
Dynamic Tokenization: The tokenization issues faced by GPT-4 highlight the need for more dynamic and flexible tokenization methods, like the xVal solution. Implementing such techniques could significantly improve the performance of general-purpose models in specialized tasks.
In a nutshell, Llemma serves as a blueprint for what specialized language models can and should be. It not only raises the bar for mathematical language models but also provides valuable insights that could benefit the broader field of artificial intelligence.
References
For those interested in diving deeper into the world of mathematical language models, here are some credible sources for further reading:
- Llemma Project GitHub Repository (opens in a new tab)
- AlgebraicStack Dataset (opens in a new tab)
- xVal Research Paper (opens in a new tab)
Want to learn the latest LLM News? Check out the latest LLM leaderboard!
